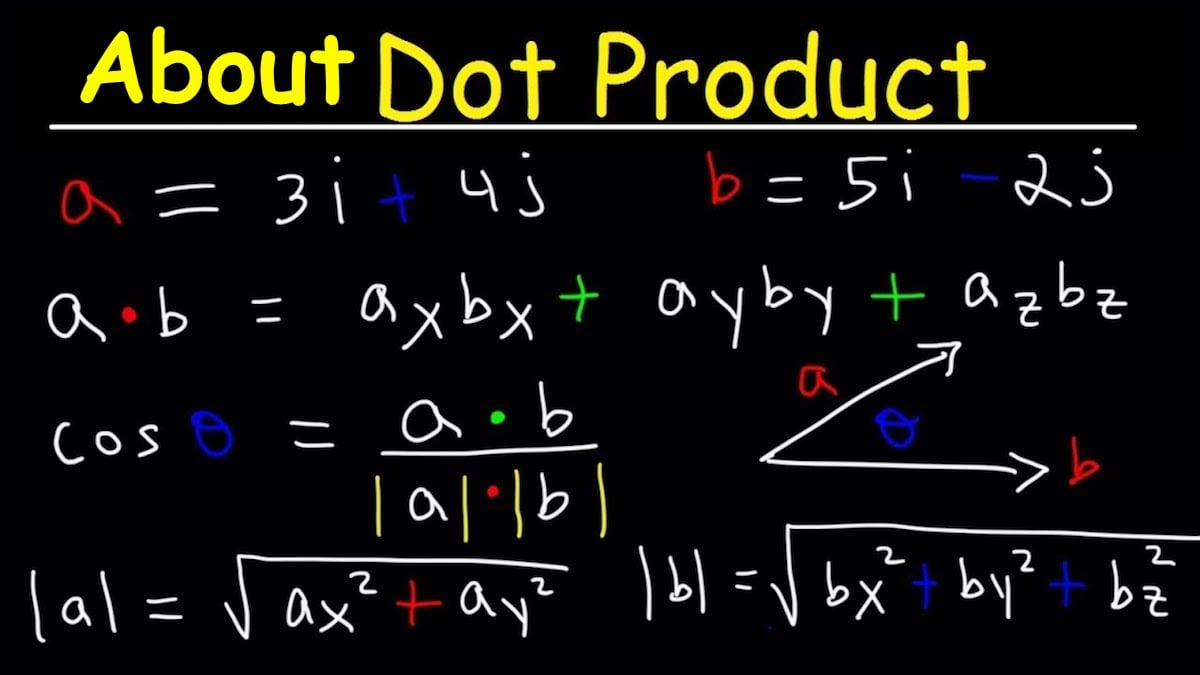
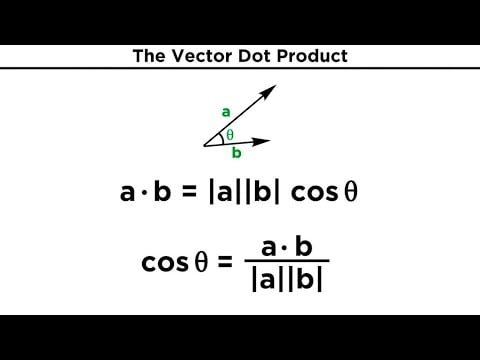
Dot products are one method of multiplying two or more vectors. The dot product of vectors produces a scalar quantity. As a result, the dot product is also referred to as a scalar product. It is the sum of the products of the corresponding entries of two number sequences. The term “dot product” can be defined in two ways: algebraically and geometrically. The dot product is defined algebraically as the sum of the products of the corresponding entries of the two number sequences. Geometrically, the dot product is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them.
About Dot Products
Geometrically, dot product is the product of two vectors’ Euclidean magnitudes and the cosine of the angle between them. The vector dot product has numerous applications in geometry, mechanics, engineering, and astronomy. In the following sections, we will go over the dot product in greater detail.
Dot Product’s Geometric Meaning
The dot product of two vectors is calculated by multiplying the component of one vector in the direction of the other by the magnitude of the other vector. To comprehend the vector dot product, we must first understand how to calculate the magnitude of two vectors and the angle between two vectors in order to calculate the projection of one vector over another vector.
What is a Vector?
A vector is defined as a quantity that has a magnitude as well as a direction. Some mathematical operations, such as addition and multiplication, can be performed on vectors. Vector multiplication can be accomplished in two ways: dot product and cross product. With the help of examples, you will learn the dot product of two vectors in this article.
Advertisement
Content in this Article
The dot product of two vectors, on the other hand, is the product of the magnitude of the two vectors and the cos of the angle between them. Vectors are multiplied in two ways, as previously stated.
- 1. Vector scalar product or vector dot product
- 2. Vector product of vectors or vector product of vectors
The only difference between the two methods is that the first yields a scalar value as a result, whereas the second yields a vector in nature. The scalar product of two vectors a and b of magnitude |a| and |b| is given as |a||b| cos θ, where θ represents the angle between the vectors a and b measured in the vectors’ direction.
The scalar product can be written as:
a.b=|a||b| cos θ
where |a| and |b| denote the magnitudes of the vectors a and b, cos θ denotes the cosine of the angle between the two vectors, and a.b denotes the dot product of the two vectors.
What is Projection of a Vector?
The dot product can be used to find the component of one vector pointing in the direction of another. The length of the shadow cast by one vector over another vector is defined as the vector projection of one vector over another vector. It is calculated by multiplying the magnitude of the given vectors by the cosecant of the angle formed by the two vectors. A scalar value is the result of a vector projection formula.
Learn Dot Products From Online Math Classes
Math is an enthralling subject. Learning Math, on the other hand, has never been easy. You can build such a solid foundation in this subject at Cuemath. If you do, Cuemath can come to your aid. It provides very low-cost online math classes. The best thing about online math classes is that they force you to visualise various problems, which helps you gain conceptual clarity.
Cuemath teachers require you to complete math worksheets as well as real-world problems, which helps you understand the significance of each chapter and relate it to practical situations. You can visit the website to develop your ideas. You can understand the basics by joining an online math class. also check High Paying Careers.